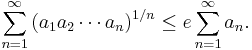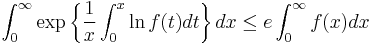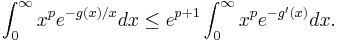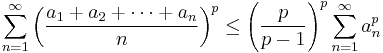Carleman's inequality
Carleman's inequality is an inequality in mathematics, named after Torsten Carleman, who proved it in 1923[1] and used it to prove the Denjoy–Carleman theorem on quasi-analytic classes.[2][3]
Contents |
Statement
Let a1, a2, a3, ... be a sequence of non-negative real numbers, then
The constant e in the inequality is optimal, that is, the inequality does not always hold if e is replaced by a smaller number. The inequality is strict (it holds with "<" instead of "≤") if all the elements in the sequence are positive.
Integral version
Carleman's inequality has an integral version, which states that
for any f ≥ 0.
Carleson's inequality
A generalisation, due to Lennart Carleson, states the following[4]:
for any convex function g with g(0) = 0, and for any -1 < p < ∞,
Carleman's inequality follows from the case p = 0.
Proof
One can prove Carleman's inequality by starting with Hardy's inequality
for the non-negative numbers a1,a2,... and p < 1, replacing each an with a1/p
n, and letting p → ∞.
Notes
- ^ T. Carleman, Sur les fonctions quasi-analytiques, Conférences faites au cinquième congres des mathématiciens Scandinaves, Helsinki (1923), 181-196.
- ^ Duncan, John; McGregor, Colin M. (2003). "Carleman's inequality". Amer. Math. Monthly 110 (5): 424–431. MR2040885.
- ^ Pečarić, Josip; Stolarsky, Kenneth B. (2001). "Carleman's inequality: history and new generalizations". Aequationes Math. 61 (1–2): 49–62. MR1820809.
- ^ Carleson, L. (1954). "A proof of an inequality of Carleman". Proc. Amer. Math. Soc. 5: 932–933.
References
- Hardy, G. H.; Littlewood. J.E.; Pólya, G. (1952). Inequalities, 2nd ed. Cambridge University Press. ISBN 0521358809.
- Rassias, Thermistocles M., editor (2000). Survey on classical inequalities. Kluwer Academic. ISBN 079236483X.
- Hörmander, Lars (1990). The analysis of linear partial differential operators I: distribution theory and Fourier analysis, 2nd ed. Springer. ISBN 354052343X.